El título está bastante trillado, pero no por eso deja de ser cierto. Hay cierta magia y belleza que no puede dejar de maravillarnos en la simpleza del interés compuesto.
Antes de explicarme, una breve introducción sobre qué estoy hablando. El interés es la retribución a uno de los factores de producción, en este caso, el capital. Es así que quien posee algún capital ahorrado, estará dispuesto a prestarlo a cambio de un interés. Luego, hay dos formas de calcularlo: régimen simple, denominado comúnmente “interés simple” o régimen compuesto denominado “interés compuesto”. Algunos podrían pensar que olvidé el régimen de interés continuo pero en realidad este es un caso extremo del que nos ocupa en este artículo.
En régimen simple estamos considerando que el interés que se va generando a lo largo del tiempo, no genera nuevos intereses en los períodos subsiguientes. Así, si yo presto $1.000 al 10%, al cabo de un año tendré $1.100 resultado de los $1.000 de capital más los $100 de interés que se generaron. Al cabo de dos años, mi monto final será de $1.200 resultado del capital inicial más $100 de interés del primer año y $100 de interés del segundo. La fórmula puede resumirse en M = C (1+i.n) donde M es el monto; C es el capital invertido; i es la tasa de interés y n es la cantidad de períodos de tiempo transcurridos.
Por su parte cuando hablamos de interés compuesto, la clave está en que el interés que se genera en un período sí genera nuevos intereses en los períodos siguientes. De esta manera es fácil apreciar que el monto al final de un determinado tiempo será mayor en régimen de interés compuesto que en el de interés simple debido a que hay intereses sobre los intereses. La fórmula es en este caso M = C (1+i)^n. Cómo vemos el “n“ en este caso está en el exponente, lo que nos dice que es una fórmula exponencial.
Con lo cual, la “belleza” o “magia” como se lo denomina es que si uno invierte su dinero a interés compuesto y deja transcurrir el tiempo podrá ver cómo se va multiplicando y creciendo exponencialmente. No en vano se dice que Albert Einstein llamo en una oportunidad al interés compuesto como “la invención más importante del mundo”
Ahora ¿cómo podemos usarlo en nuestro provecho? Hay una regla muy simple que todo el mundo debería conocer y se la denomina como la Regla del 72. Esto no es otra cosa que una forma sencilla de aproximar cuanto tiempo se necesitará para duplicar un capital a una determinada tasa de interés. Obviamente es una aproximación, pero con un alto grado de exactitud. También cuenta la leyenda que fue el mismo Einstein quien descubrió esta regla y exclamó que era el descubrimiento matemático más grande de la historia. Yo creo que exagera, pero al menos es muy interesante.
La forma de cálculo es muy sencilla: si quiero saber cuántos años necesito para duplicar mi dinero con una determinada tasa de interés sólo tengo que dividir 72 por la tasa de interés. Veamos: si invierto mi dinero a una tasa del 10% anual, ¿cuantos años necesitaré para duplicarlo? La respuesta la encontramos dividiendo 72 por 10 y nos da 7,2 años. O sea invirtiendo durante 7,2 años al 10% anual, al final de ese período lo habré duplicado. De hecho en realidad lo habré aumentado en un 99% (no exactamente el 100%) pero perdónesele a la formula el error mínimo en virtud de la calidad de la información que nos brinda.
De la misma forma, si lo que quiero es saber a qué tasa tengo que invertir un capital para duplicarlo en un determinado número de años, solo tengo que dividir 72 por la cantidad de años en cuestión. Por ejemplo si quiero duplicar mi dinero en 6 años deberé dividir 72 por 6. El resultado me dice que necesitaré una tasa de interés del 12% anual para lograr mi meta.
En la siguiente tabla se podrá apreciar bien las diferencias entre los dos regímenes y la regla del 72 en acción. Desarrollamos una inversión de $1.000 en tres escenarios diferentes de tasas al 6%, 12% y 18%. Luego calculamos cual sería el monto final al cabo de diferentes períodos de tiempo desde 0 a 30 años.
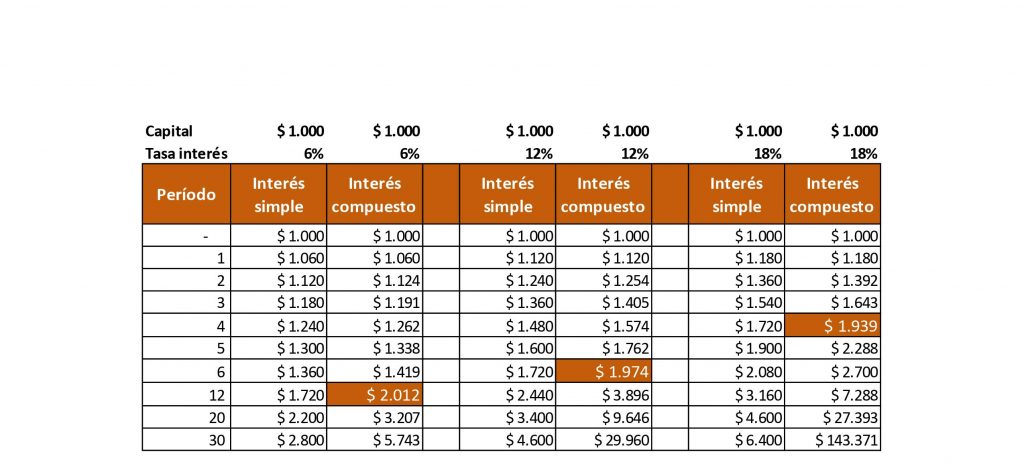
De la tabla se pueden sacar varias conclusiones interesantes. Como se puede apreciar, siempre el monto a interés compuesto es mayor que a interés simple. Pero vemos que la diferencia es mayor cuanto mayor es la tasa y cuanto mayor es el paso del tiempo.
Por otro lado también vemos cómo funciona la regla del 72. Los cuadrados pintados son aquellos en donde se verifica. Y como se ve, si bien no se duplica exactamente, el resultado es muy cercano.
Para terminar este artículo un par de anécdotas que ilustran perfectamente esta magia de la que hablamos. Los protagonistas principales son los indios que habitaban la isla de Manhattan cuando los europeos llegaron a colonizarlos. Se dice que fue Peter Mint quien en 1626 compró la tierra de lo que hoy es la isla de Manhattan (lugar caro en el mundo si los hay) para fundar Nueva Amsterdam. En ese entonces el pago consistió en baratijas cercanas a la suma de 24 dólares y fue claramente una estafa. Ahora ¿Qué hubiera pasado si los indios hubieran invertido ese dinero hasta el día de hoy? Vemos que desde 1.626 hasta hoy han transcurrido 386 años. Si suponemos una tasa de interés del 8%, el monto ascendería a aproximadamente USD 191.000.000.000.000.- No es un error, es un 191 seguido de 12 ceros, un número casi innombrable que seguramente podría comprar varias veces la mencionada isla.
Otra anécdota es el discurso que el cacique Guaicaipuro Cuautemoc pronunció en febrero de 2.002 ante los jefes de la Comunicad Económica Europea[1]. No lo vamos a incluir integro pero resumiendo dice que América le concedió a Europa un préstamo 185.000 kilos de oro y 16 millones de kilos de plata hace 500 años. En su discurso dice “…Nos limitaremos a exigir la devolución de los metales preciosos adelantados, más el módico interés fijo del 10 por ciento, acumulado sólo durante los últimos 300 años, con 200 años de gracia. Sobre esta base, y aplicando la fórmula europea del interés compuesto, informamos a los descubridores que nos deben, como primer pago de su deuda, una masa de 185 mil kilos de oro y 16 millones de plata, ambas cifras elevadas a la potencia de 300…” ¿Se entiende el número del que hablamos? ¡A la potencia de 300!
Obviamente que lo narrado no supera el territorio de lo anecdótico, ya que nadie le serviría esperar tantos años para cobrar, pero es una forma más que elocuente de evidenciar el poder de la capitalización. Y lo bueno es que todos lo podemos usar en nuestro favor. Sólo hay que tener en cuenta a la hora de gastarnos la renta de alguna inversión, que mejor la reinvertimos y el tiempo se encargará de hacer el trabajo por nosotros.
__________________________________________________________________________________________







